数据结构与算法 — 递归

前言

递归是算法中一种非常重要的思想，应用非常广泛。是DFS、分治法、回溯、二叉树遍历等方法的基础。先从学习这些方法的基础开始。

什么是递归

程序调用自身的编程技巧称为递归（ recursion）。一个过程或函数在其定义或说明中有直接或间接调用自身的一种方法，它通常把一个大型复杂的问题层层转化为一个与原问题相似的规模较小的问题来求解。

像下面这样直接调用自身的函数：

function recursion(param){
    recursion(param)
}

间接调用自身的函数，也是递归函数：

function recursion1(param){
    recursion2(param)
}

function recursion2(param){
    recursion1(param)
}

假设现在执行 recursion 函数，就上述情况而言，其会一直执行下去。因此，每个递归函数都必须要有边界条件，即一个不再递归调用的条件，以防止无限递归。

如果忘记加上用以停止函数递归调用的边界条件，在浏览器中执行，递归并不会无限地执行下去，浏览器会抛出错误 Maximum call stack size exceeded 也就是所谓的栈溢出。

以阶乘为例，体会一下递归：

function factorial(n) {
    if (n <= 1) {
        return 1
    }
    return n * factorial(n - 1)
}

factorial(6) // 6 * 5 * 4 * 3 * 2 * 1 = 720

factorial 是一个实现阶乘的函数，来看下它的调用过程。

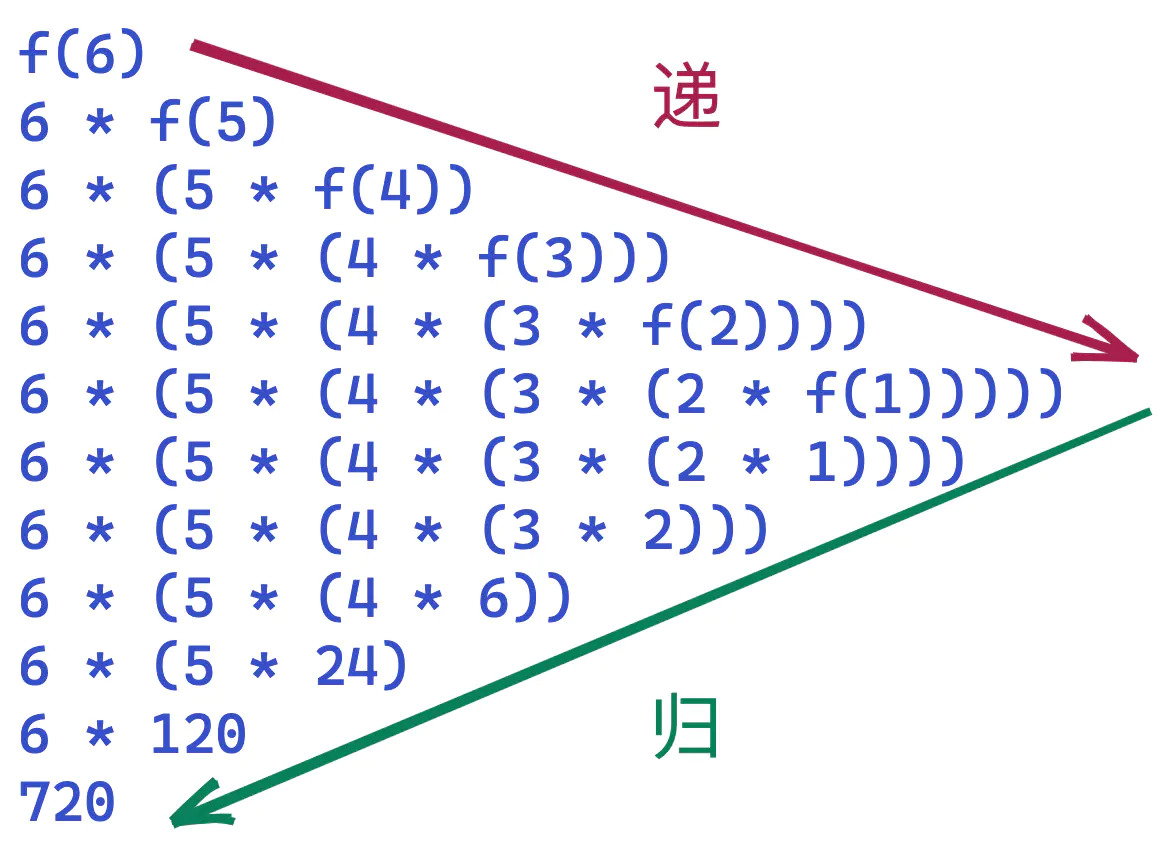
从这个例子中可以看出，阶乘中的 n <= 1 是边界条件，当边界条件不满足时，递归前进，当边界条件满足时，递归返回。构成递归需具备边界条件、递归前进段和递归返回段。

斐波那契数列

斐波那契指的是这样一个数列：1、1、2、3、5、8、13、21、34 ...，这个数列从第3项开始，每一项都等于前两项之和。

递归实现

function fibonacci(n) {
    if (n <= 2) {
        return 1
    }
    return fibonacci(n - 1) + fibonacci(n - 2)
}

console.log(fibonacci(6)) // 8

但是当参数 n 变大时，浏览器卡死了。原因是此函数中存在着大量的冗余计算，并且 n 越大，冗余的越多。如下图所示：

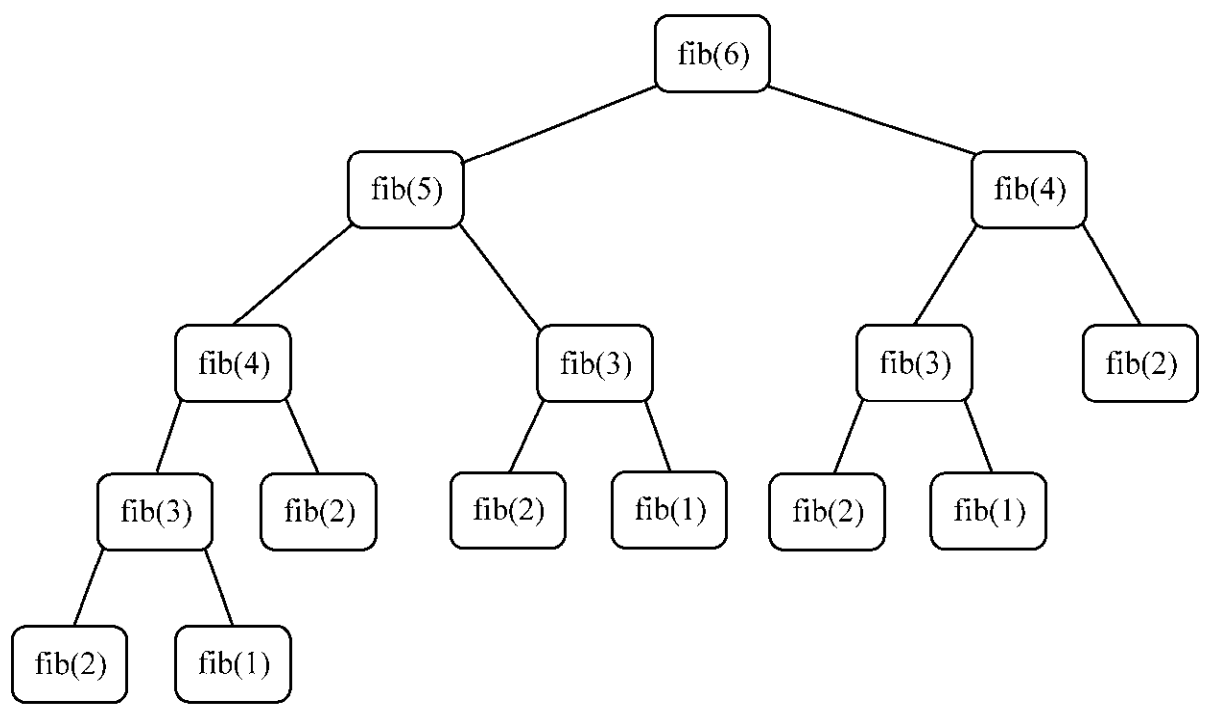
图中每个分支上的函数都是单独调用的，并且都是重复的调用，针对这种冗余计算，我们可以做相关的优化，优化的思路都是减少相同函数的重复调用。

迭代实现

function fibonacci(num){
    var n1 = 1,
    n2 = 1,
    n = 1;
    for (var i = 3; i <= num; i++){
        n = n1 + n2;
        n1 = n2;
        n2 = n;
    }
    return n;
}

尾调用优化

function fibonacci (n, res1 = 1, res2 = 1) {
    if (n <= 2) {
        return res2
    }
    return fibonacci(n - 1, res2, res1 + res2)
}

应用场景

一些 JavaScript 的工具方法中涉及到了递归。

深拷贝

function deepCopy (data) {
    // 数据类型判断函数，见下
    const t = typeOf(data)
    let o

    if (t === 'array') {
        o = []
    } else if (t === 'object') {
        o = {}
    } else {
        return data
    }

    for (var key in data) {
        o[key] = deepCopy(data[key])
    }

    return o
}

function typeOf (obj) {
    const toString = Object.prototype.toString
    const map = {
        '[object Boolean]': 'boolean',
        '[object Number]': 'number',
        '[object String]': 'string',
        '[object Function]': 'function',
        '[object Array]': 'array',
        '[object Date]': 'date',
        '[object RegExp]': 'regExp',
        '[object Undefined]': 'undefined',
        '[object Null]': 'null',
        '[object Object]': 'object'
    }
    return map[toString.call(obj)]
}

数组扁平化

function flatten(arr) {
    return arr.reduce(function(prev, next){
        return prev.concat(Array.isArray(next) ? flatten(next) : next)
    }, [])
}

总结

学习了递归的基本使用和实现了 JavaScript 中常用的工具方法。关于递归的内容还有很多，比如还有汉诺塔、二叉树遍历等递归场景。算法之路漫漫 😬。

Rubin's Blog