前言
程序 = 数据结构 + 算法
要想在编程之路走的更远,学好数据结构与算法很重要。所以把学习的总结写成一个系列,使用自己熟悉的 JavaScript 语言,旨在入门数据结构与算法和方便以后复习。
先从算法领域里基础的排序算法开始。
经典排序算法对比
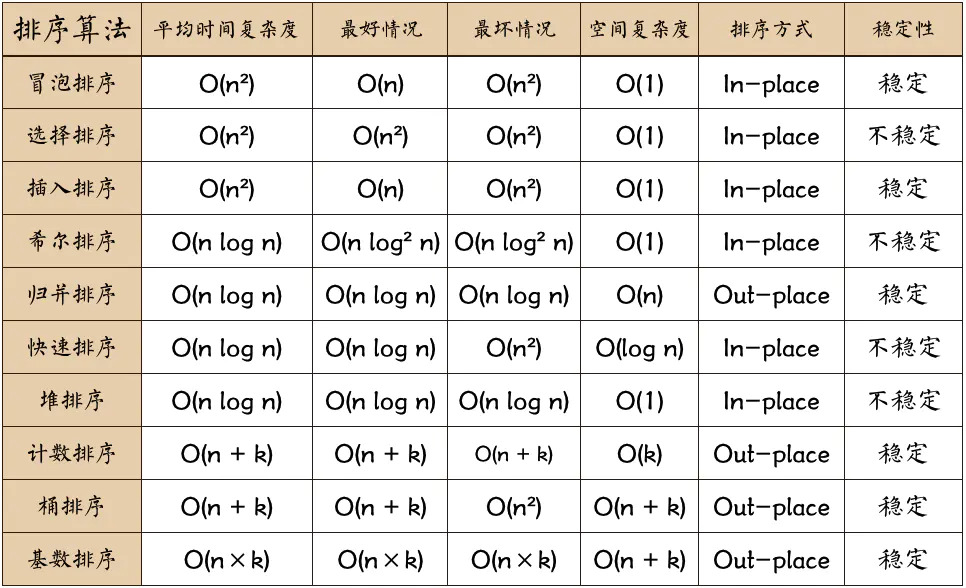
名词解释:
n: 待排序列的个数
k: “桶”的个数
In-place: 原地算法,指的是占用常用内存,不占用额外内存。空间复杂度为 O(1) 的都可以认为是原地算法
Out-place: 非原地算法,占用额外内存
稳定性:排序后2个相等键值的顺序和排序之前它们的顺序相同
冒泡排序
冒泡排序是一种简单的排序算法。它重复地走访过要排序的数列,一次比较两个元素,如果它们的顺序错误就把它们交换过来。走访数列的工作是重复地进行直到没有再需要交换,也就是说该数列已经排序完成。这个算法的名字由来是因为越小的元素会经由交换慢慢“浮”到数列的顶端。
算法描述:
- 比较相邻的元素。如果第一个比第二个大,就交换它们两个。
- 对每一对相邻元素作同样的工作,从开始第一对到结尾的最后一对,这样在最后的元素应是最大的数。
- 针对所有的元素重复以上的步骤,除了最后一个。
- 重复步骤1~3,直到排序完成。
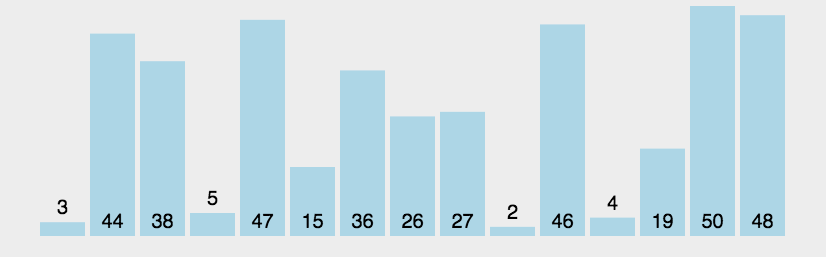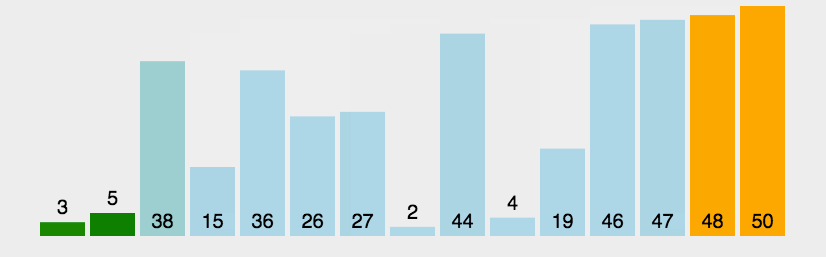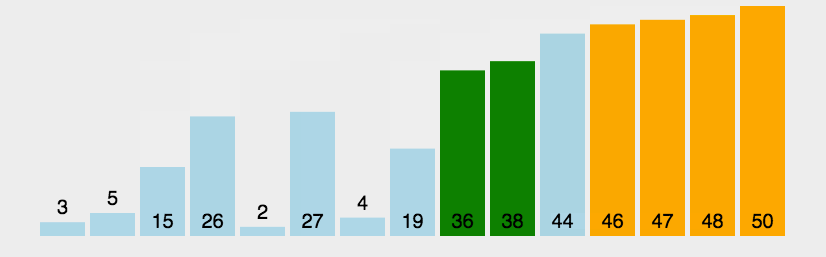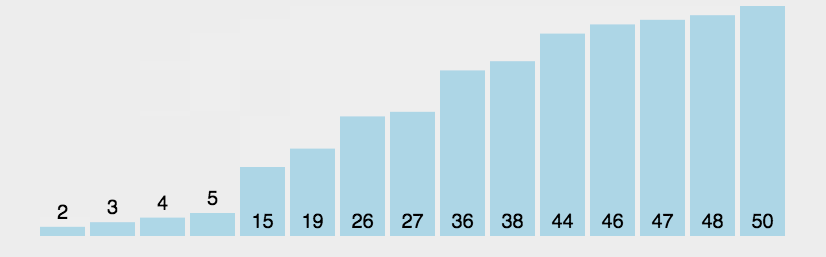
代码实现:
function bubbleSort(array) {
var length = array.length
for (var i = 0; i < length; i++) {
// length - 1 - i 从内循环减去外循环中已跑过的轮数,就可以避免内循环中所有不必要的比较
for (var j = 0; j < length - 1 - i; j++) {
// 如果当前项比下一项大,则使用中间值进行交换
if (array[j] > array[j + 1]) {
var temp = array[j]
array[j] = array[j + 1]
array[j + 1] = temp
}
}
}
return array
}
bubbleSort([3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48])
// [2, 3, 4, 5, 15, 19, 26, 27, 36, 38, 44, 46, 47, 48, 50]
选择排序
选择排序算法是一种原址比较排序算法。选择排序大致的思路是找到数据结构中的最小值并
将其放置在第一位,接着找到第二小的值并将其放在第二位,以此类推。
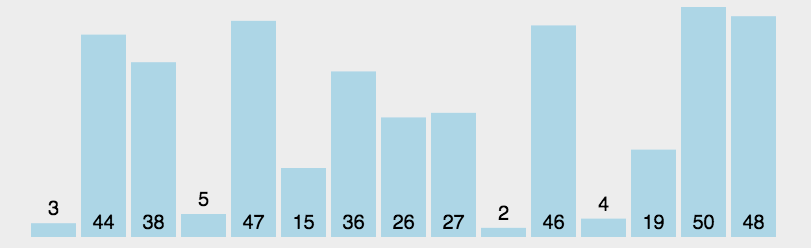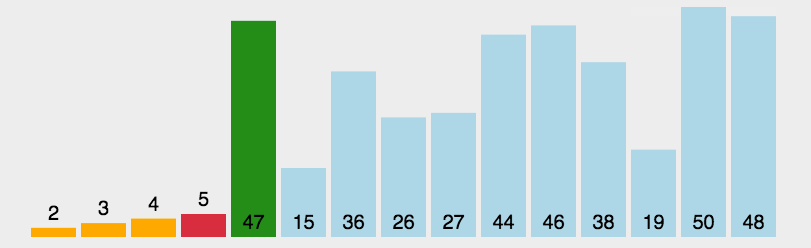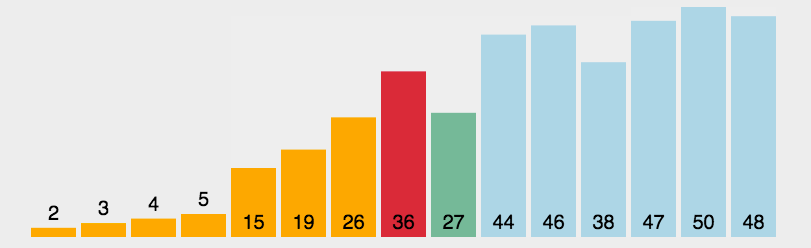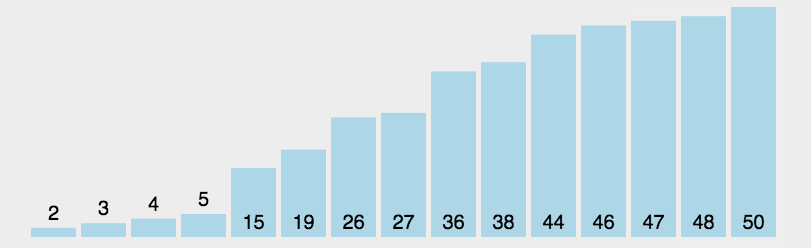
代码实现:
function selectionSort (array) {
var length = array.length
var minIndex, temp
for (var i = 0; i < length - 1; i ++) {
minIndex = i // 假设本次循环的第一个值为数组最小值
for (var j = i + 1; j < length; j++) {
// 比较位置j的值是否比当前最小值小
if (array[j] < array[minIndex]) {
minIndex = j // 如果是,则改变最小值的索引
}
}
// 如果该最小值和原最小值不同,则交换其值
if (i !== minIndex) {
temp = array[i]
array[i] = array[minIndex]
array[minIndex] = temp
}
}
return array
}
selectionSort([3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48])
// [2, 3, 4, 5, 15, 19, 26, 27, 36, 38, 44, 46, 47, 48, 50]
选择排序同样也是一个复杂度为 的算法。和冒泡排序一样,它包含有嵌套的两个循环,这导致了二次方的复杂度。
插入排序
插入排序每次排一个数组项,以此方式构建最后的排序数组。假定第一项已经排序了。取第二项向前进行比较,第二项是应该待在原位还是插到第一项之前呢?这样,头两项就已正确排序,接着和第三项比较(它是该插入到第一、第二还是第三的位置呢?),以此类推。
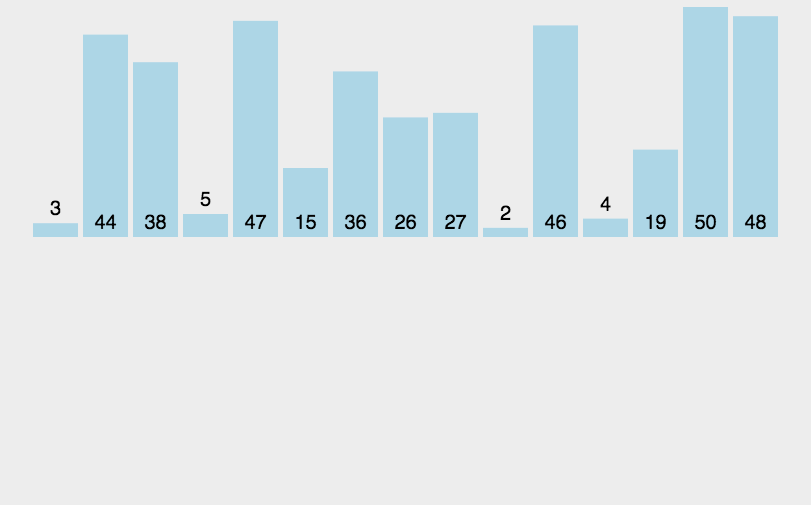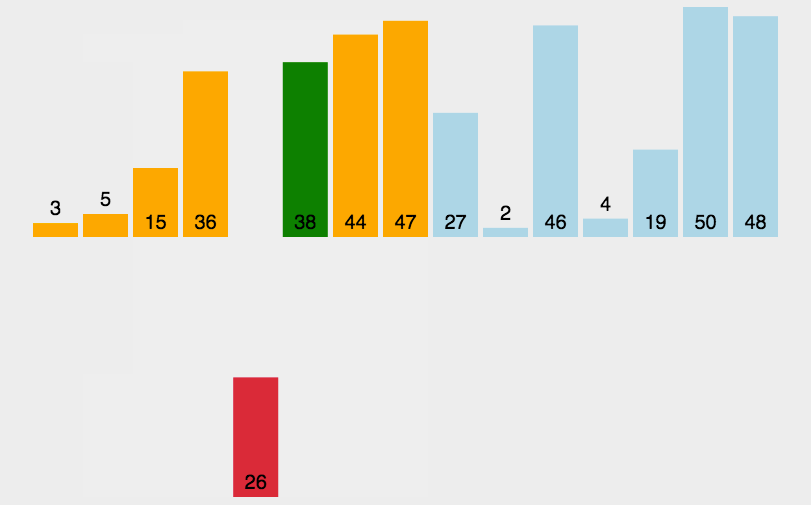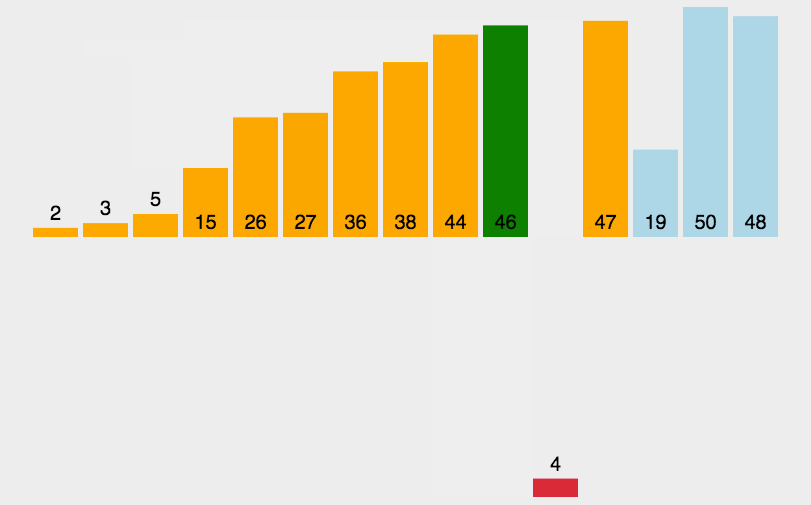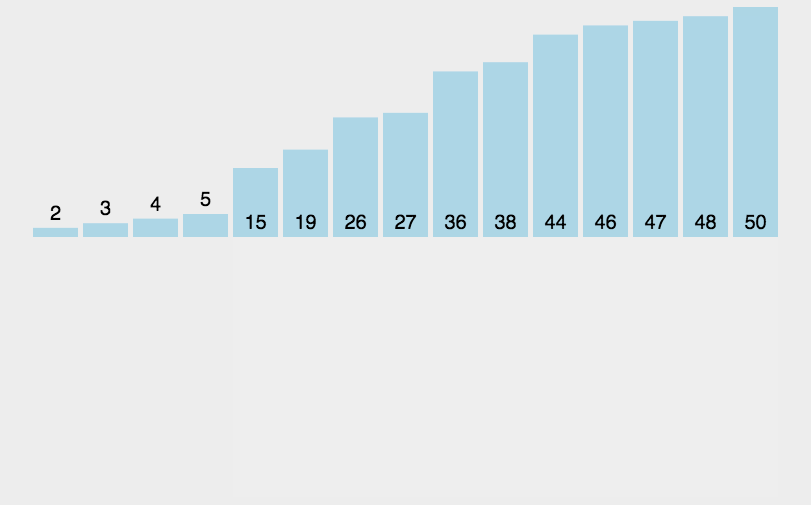
代码实现:
function insertionSort (array) {
var length = array.length
var j, temp
// 是从第二个位置(索引1)而不是0位置开始的(假定第一项已排序了)
for (var i = 1; i < length; i ++) {
// 用i的值来初始化一个辅助变量并将其值亦存储于一临时变量中,便于之后将其插入到正确的位置上
j = i
temp = array[i]
// 要变量j比0大,并且数组中前面的值比待比较的值大
// 就把这个值移到当前位置上并减小j
while (j > 0 && array[j - 1] > temp) {
array[j] = array[j - 1]
j--
}
array[j] = temp
}
return array
}
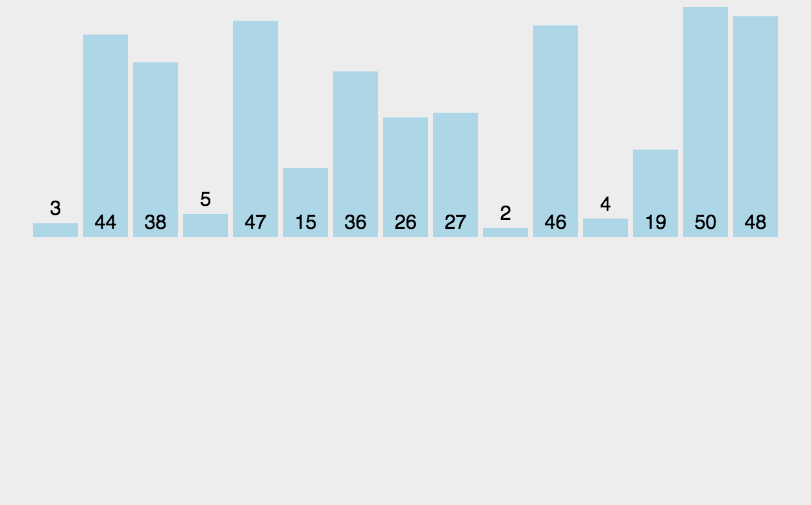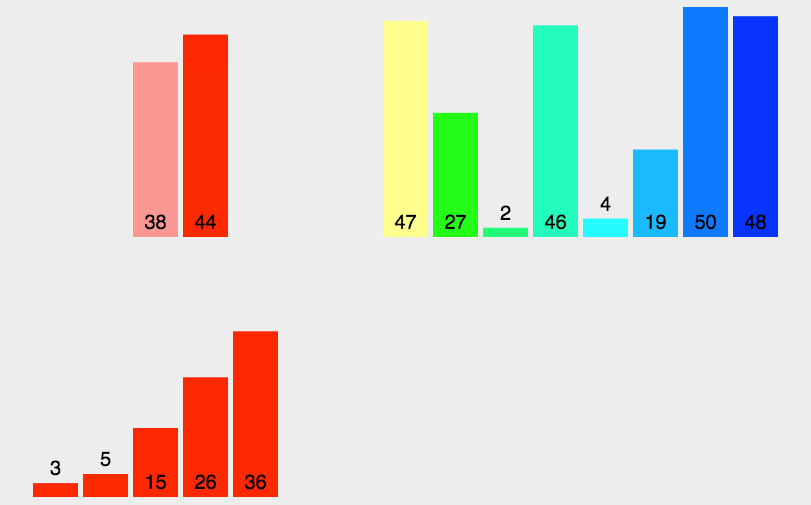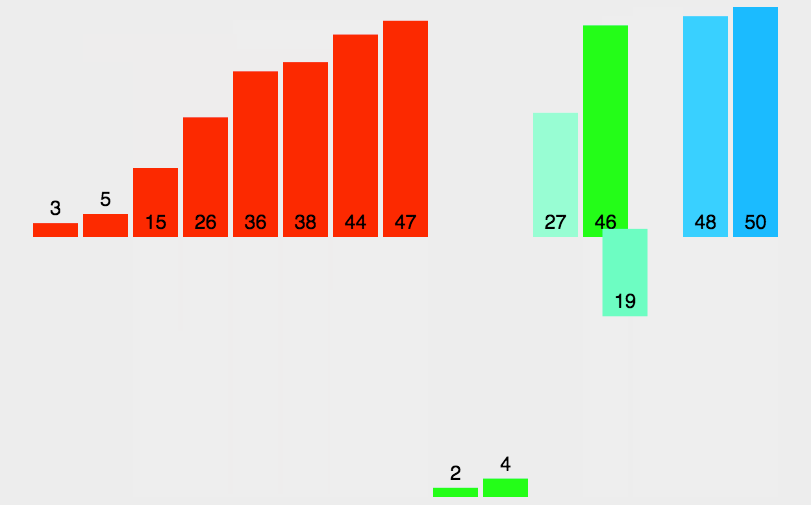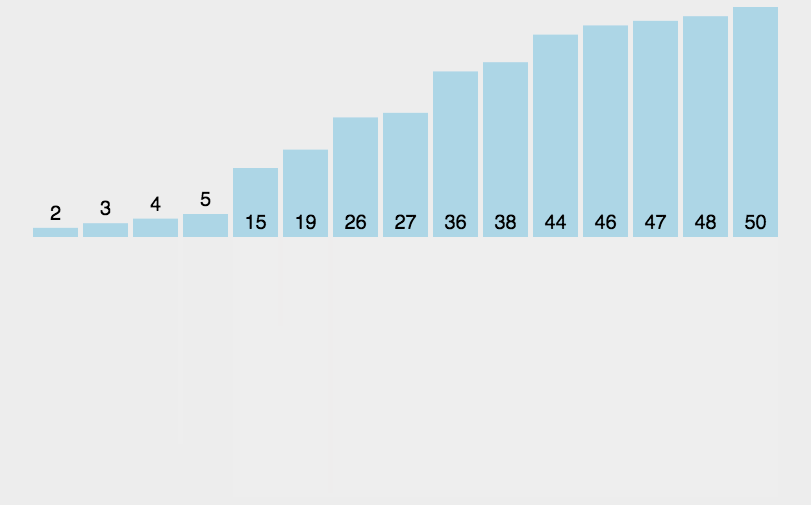
归并排序
归并排序是一种分治算法。其思想是将原始数组切分成较小的数组,直到每个小数组只有一
个位置,接着将小数组归并成较大的数组,直到最后只有一个排序完毕的大数组。
代码实现:
function mergeSort (array) {
var length = array.length
// 由于算法是递归,需要一个停止条件
if (length <= 1) {
return array
}
// 如果数组长度大于1,首先是找到数组的中间位,之后将数组分成left、right两个小数组
var mid = Math.floor(length / 2)
var left = array.slice(0, mid)
var right = array.slice(mid)
// 调用merge函数,它负责合并和排序小数组来产生大数组
// 为了不断将原始数组分成小数组,我们得再次对left数组和right数组递归调用mergeSort,并同时作为参数传递给merge函数
return merge(mergeSort(left), mergeSort(right))
}
function merge (left, right) {
// 声明归并过程要创建的新数组以及用来迭代两个数组(left和right)所需的两个变量
var result = [], il = 0, ir = 0
// 迭代两个数组的过程中,比较两个数组的项大小。将小的一方添加至结果数组,并递增迭代数组的控制变量
while (il < left.length && ir < right.length) {
if (left[il] < right[ir]) {
result.push(left[il++])
} else {
result.push(right[ir++])
}
}
// 接下来,分别将两个数组剩余的项添加到结果数组中
while (il < left.length) {
result.push(left[il++])
}
while (ir < right.length) {
result.push(right[ir++])
}
return result;
}
mergeSort([3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48])
归并排序性能不错,其复杂度为 。
快速排序
快速排序是最快的排序算法之一,它的复杂度为 。和归并排序一样,快速排序也使用分治的方法,将原始数组分为较小的数组。
算法描述:
- 从数组中选择中间一项作为“主元”(pivot)。
- 创建两个指针,左边一个指向数组第一个项,右边一个指向数组最后一个项。移动左指
针直到我们找到一个比主元大的元素,接着,移动右指针直到找到一个比主元小的元素,然后交
换它们,重复这个过程,直到左指针超过了右指针。这个过程将使得比主元小的值都排在主元之
前,而比主元大的值都排在主元之后。这一步叫作划分操作(partition)。 - 算法对划分后的小数组(较主元小的值组成的子数组,以及较主元大的值组成的
子数组)重复之前的两个步骤,直至数组已完全排序。
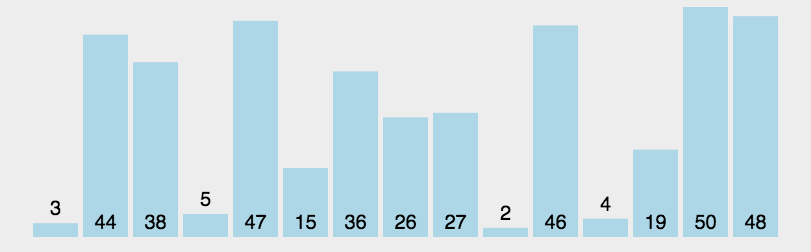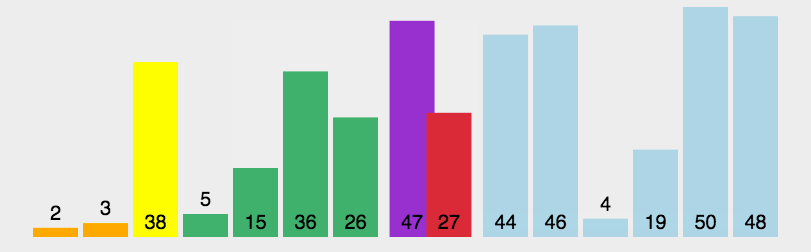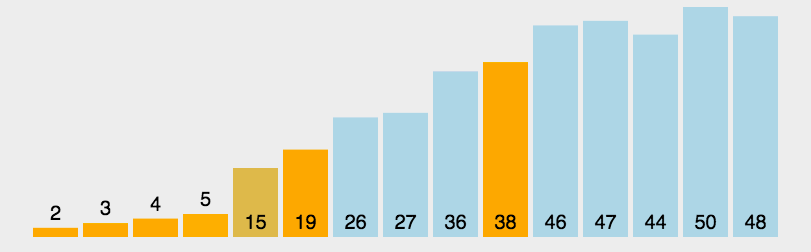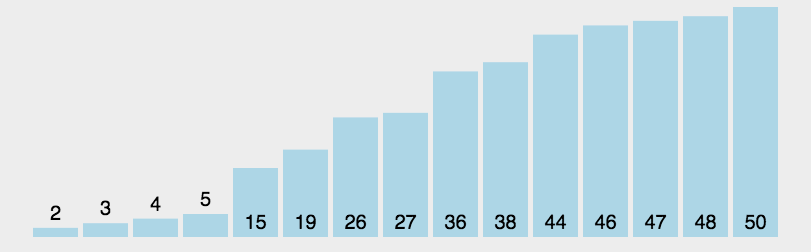
代码实现:
function quickSort(array) {
// 传递待排序数组,以及索引0及其最末的位置(因为我们要排整个数组,而不是一个子数组)作为参数
return quick(array, 0, array.length - 1)
}
function quick(array, left, right) {
// 声明index变量,用于帮助我们将子数组分离为较小值数组和较大值数组
var index
if (array.length > 1) {
index = partition(array, left, right)
// 划分为两个子数组重复快速排序过程
if (left < index - 1) {
quick(array, left, index - 1)
}
if (index < right) {
quick(array, index, right)
}
}
return array
}
function partition(array, left, right) {
// 选择中间项作为主元,初始化两个指针:数组第一个元素、数组最后一个元素
var pivot = array[Math.floor((left + right) / 2)],
l = left,
r = right;
// 只要left和right指针没有相互交错,就执行划分操作
while (l <= r) {
// 移动left指针直到找到一个元素比主元大
while (array[l] < pivot) {
l++
}
// 移动right指针直到找到一个元素比主元小
while (array[r] > pivot) {
r--
}
// 当左指针指向的元素比主元大且右指针指向的元素比主元小,并且此时左指针索引没有右指针索引大,则交换它们,然后移动两个指针,并重复此过程继续循环。
if (l <= r) {
var temp = array[l]
array[l] = array[r]
array[r] = temp;
l++
r--
}
}
// 在划分操作结束后,返回左指针的索引,用来处创建子数组
return l
}
quickSort([3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48])
堆排序

代码实现:
function heapSort(array) {
var heapSize = array.length
for (var i = Math.floor(heapSize / 2); i >= 0; i--) {
heapify(array, heapSize, i)
}
while (heapSize > 1) {
heapSize--
swap(array, 0, heapSize)
heapify(array, heapSize, 0)
}
return array
}
function heapify(array, heapSize, i) {
var left = i * 2 + 1,
right = i * 2 + 2,
largest = i;
if (left < heapSize && array[left] > array[largest]) {
largest = left;
}
if (right < heapSize && array[right] > array[largest]) {
largest = right;
}
if (largest !== i) {
swap(array, i, largest);
heapify(array, heapSize, largest);
}
}
function swap(arr, i, j) {
var temp = arr[i]
arr[i] = arr[j]
arr[j] = temp
}
heapSort([3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48])
总结
感慨算法实在是博大精深,前辈们花费心血研究出的成果值得我们学习和推敲。排序算法还有计数排序、桶排序和基数排序,实在没精力去一一研究了😓。